ストークスの定理
slot asia77 smart matkaストークスの定理とは?[例題つき] - 大学の知識で学ぶ電気電子工学. ストークスの定理は、ベクトル場と曲面の接線線積分と法線面積分を足し合わせることで、閉じた経路の接線線積分と法線面積分を求めることです。この記事では、ストークスの定理の直観的なイメージや例題を紹介し、保存力やスカラーポテンシャルの関係についても説明します。. ストークスの定理 - Wikipedia. ストークスの定理 (ストークスのていり、 英: Stokes theorem )は、 ベクトル解析 の 定理 のひとつである。 3次元 ベクトル場 の 回転 を 閉曲線 を境界とする 曲面 上で面積分したものが、元のベクトル場を曲面の境界である閉曲線上で 線積分 したものと一致することを述べる [1] 。 定理の名はイギリスの物理学者 ジョージ・ガブリエル・ストークス に因む [2] [3] 。 ベクトル解析における グリーンの定理 、 ガウスの定理 、 ストークスの定理 を、より一般的な向きづけられた 多様体 上に拡張したものも、同様にストークスの定理と呼ばれる。 微分積分学の基本定理 の、多様体への拡張であるともいえる。 ストークスの定理 詳細は「 ケルビン・ストークスの定理 」を参照. ガウスの発散定理・ストークスの定理の証明 | 高校数学の美しい物語. ガウスの発散定理とストークスの定理は、閉曲面の面積分を分割して和をとると、閉曲面の面積分の和が閉曲面の面積分に等しいことを証明する公式です。この記事では、ガウスの発散定理とストークスの定理の証明を4ステップに分けて説明し、線積分の意味や例題も解説します。. 【ベクトル解析】ストークスの定理~概要と例題~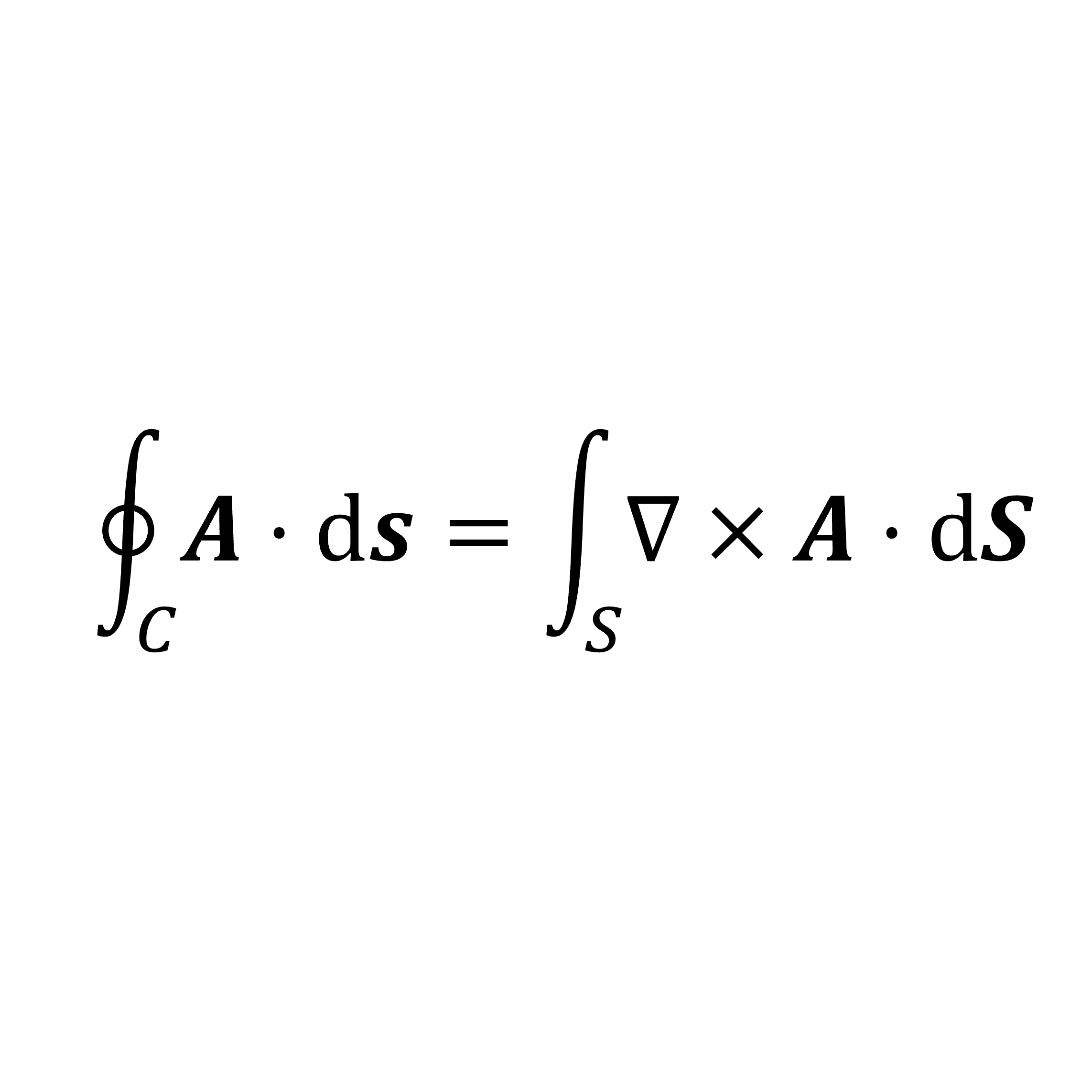
keadaan cuaca di penang fond de teint phoera
. ストークスの定理【内容と証明】 | 理数系学習サイト kori. ストークスの定理は、ベクトル場の 接線線積分 と、ベクトル場の回転に対する 法線面積分 を等式で結びつける事ができるという数学上の定理です。 その内容と証明について詳しく説明します。 定理の内容と表記 ベクトル場の変数x、y、zは独立変数で、ベクトル場の回転の計算(偏微分含む)もまずその条件下で行われます。 次に、対象となる関数を積分する時点で曲面上あるいは曲線上という制約がつく…すなわちz=z (x,y)といった形の式が一部の変数に代入されて互いに独立ではなくなるとします。 ベクトル場はF→ = (F1(x, y, z),F2(x, y, z),F3(x, y, z))であるとします。 曲面S上でz = z(x, y)という制約がつく時はtypirec plus para que sirve www.x videos.com
. ストークスの定理の証明 - Emanの電磁気学. ストークスの定理はベクトルの回転を表す量と線積分を面積分に変換する公式で、ガウスの定理に似ているが、完全に納得するためにはガウスの定理より少々の根気が必要かもしれない. この記事では、ストークスの定理の式と意味、教科書の説明と説明を学生時代の自分に届けてやりたいということを目指している.. ストークスの定理 [物理のかぎしっぽ]. ガウスの定理,平面のグリーンの定理などと並んで,ベクトル解析分野で最も重要な積分定理が,この ストークスの定理 です.ストークスの定理は,三次元の曲面とその曲面上で定義された関数に関し,線積分と面積分を関係づける定理です. 【ストークスの定理】閉曲線 を境界とする曲面 上で, 級ベクトル値関数 が定義されています.ただし は単連結とします.このとき が成り立ちます.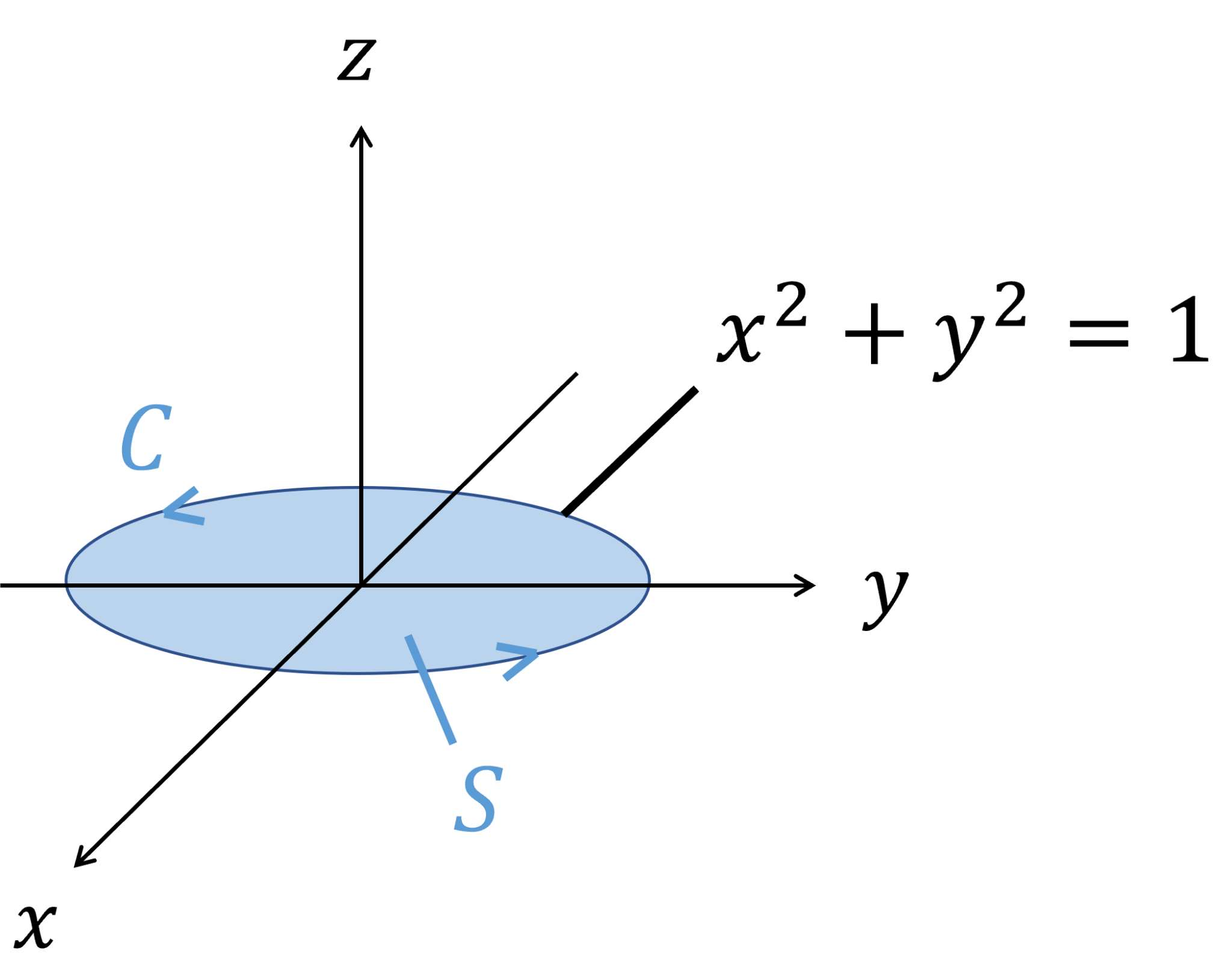
loto 6/49 17.03.2016 sambal goreng pengantin
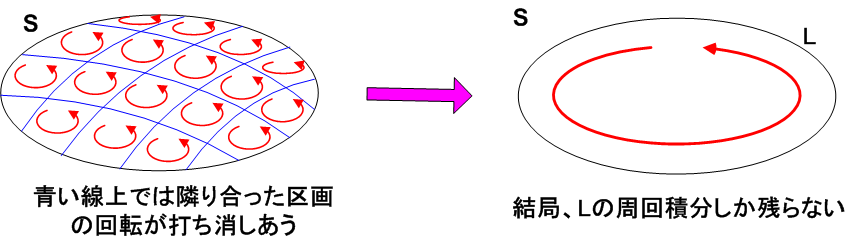
. ストークスの定理は、閉曲線 C C を境界とする曲面 S S において、閉曲線の偏導関数 F の回転の法線面積分を求めることで、閉曲線の法線面積分を求めることで求められる。この定理は、閉曲線の法線面積分と偏導関数の法線面積分の関係を表すとともに、閉曲線の法線面積分を求めることで閉曲線の法線面積分を求めることで求められる。. ストークスの定理 意味と証明【ベクトル解析】 | みやちゃのブログ. ストークスの定理は、曲面の端の経路線積分と微小面積の法線ベクトル方向の回転の和を積分できることを示すベクトル解析の定理です。回転の意味や積分計算の方法を図解して説明しています。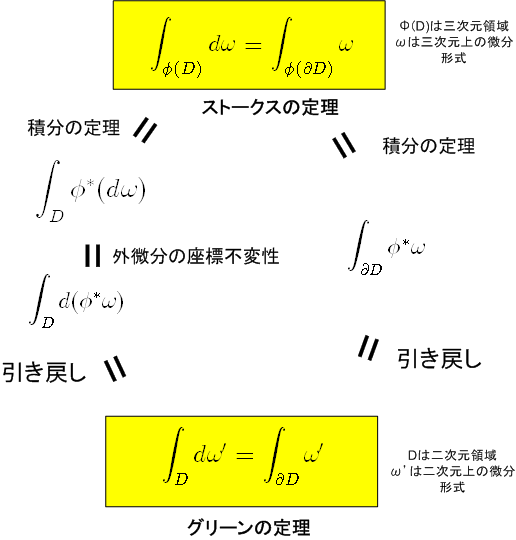
ramaln cuaca hari ini xəstəlik vərəqəsi iş yerinə təqdim edilməyənə qədər tabeldə iş günləri necə qeyd edilir?
. ストークスの定理 ストークスの定理 とは、以下のような定理である。 ストークスの定理 F → ( x, y, z) はベクトル場、 S は R 3 内の(有界な)曲面、 ∂ S は S の境界とする。 このとき、 V 内の任意の点で ∇ × F → が定まるならば ∫ ∂ S F → ⋅ d r → = ∫ S ( ∇ × F →) ⋅ d S → である。 ただし、 S の向きに対して ∂ S は右ねじの向きとする。 ストークスの定理において、左辺は曲線 ∂ S 上での線積分、右辺は S 上の面積分になっている。 つまり、ストークスの定理とは 線積分と面積分をつなぐ定理 である。 定理の意味ekocheras karaoke price 10 év után végkielégítés


cfare eshte hernia diskale cum public o procedura simplificata
. PDF ベクトル解析 - Tokushima U蟲草19 lenjeh artinya
. グリーンの定理 {10{ ストークスの定理の特別な場合として、曲面がxy 平面内にある ときグリーンの定理が成り立つ. 定理 D をxy平面の有界な領域で,その境界C は互いに交わら ない有限個の区分的にC1 級の単一閉曲線からなっているとする. そのときD を含む開集合でC1 級の関数f(x;y);g(x;y)に対して. ケルビン・ストークスの定理 - Wikipedia. (2018年12月) 下記テーマに関する記事の一部 解析学 基本定理 関数の極限 連続性 平均値の定理 微分法 積分法 級数 ベクトル 多変数 特殊化 その他 表 話 編 歴 ケルビン・ストークスの定理 (ケルビン・ストークスのていり、 英: Kelvin-Stokes theorem ) [1] [2] [3] [4] [5] [6] [7] [8] は、3次元 ベクトル場 の2次元曲面上での 面積分 に関する定理であり、本定理は、与えられたベクトル場の回転を面積分したものと、前記面積分の積分領域の境界での線積分とを関連付ける。my girlfriend is a gumiho dramanice 蜂 防護服 ワークマン
. ストークスの定理 - Wikiwand. ストークスの定理 (ストークスのていり、 英: Stokes theorem )は、 ベクトル解析 の 定理 のひとつである。 3次元 ベクトル場 の 回転 を 閉曲線 を境界とする 曲面 上で面積分したものが、元のベクトル場を曲面の境界である閉曲線上で 線積分 したものと一致することを述べる 。 定理の名はイギリスの物理学者 ジョージ・ガブリエル・ストークス に因む 。 ベクトル解析における グリーンの定理 、 ガウスの定理 、 ストークスの定理 を、より一般的な向きづけられた 多様体 上に拡張したものも、同様にストークスの定理と呼ばれる。 微分積分学の基本定理 の、多様体への拡張であるともいえる。 ストークスの定理 詳細は「 ケルビン・ストークスの定理 」を参照. ベクトル解析入門⑪ ~ストークスの定理~ - YouTube. 今回はストークスの定理です。ベクトル解析入門シリーズ①基本ベクトル・内積・外積 outu.be/cB38FzDgc0c②曲線・前編 .. ストークスの定理 - Tsukuba. ストークスの定理. ストークスの定理は 線積分を面積分に変換する定理 で,前述のガウスの定理と並んで電磁気学において最もよく利用される数学上の定理である.すなわち,次の任意のベクトル場 ( ),. を考えたとき,. (1.4.58) の関係が成り立つ.unix789 yuxuda adam öldürmek görmek
. 図 1.15 .. ストークスの定理 | technical-note. 定理. 3次元空間において $boldsymbol{v}(boldsymbol{x})$:滑らかなベクトル関数 $C$:空間内の閉曲線 $S$:閉曲線 $C$ を境界とする .. 【神戸ストークス】M・ヒサタケが攻守に活躍、チーム得点王が離脱(サンテレビ) - Yahoo!ニュース. ストークスは序盤、キャプテン道原紀晃の2本の3ポイントシュートなどで波に乗り、ゴール下に走り込んだ選手に速いパスを通して得点したり ..